1DTupleInterpolation
Repository source: 1DTupleInterpolation
Description¶
Contributed by: Lars Friedrich
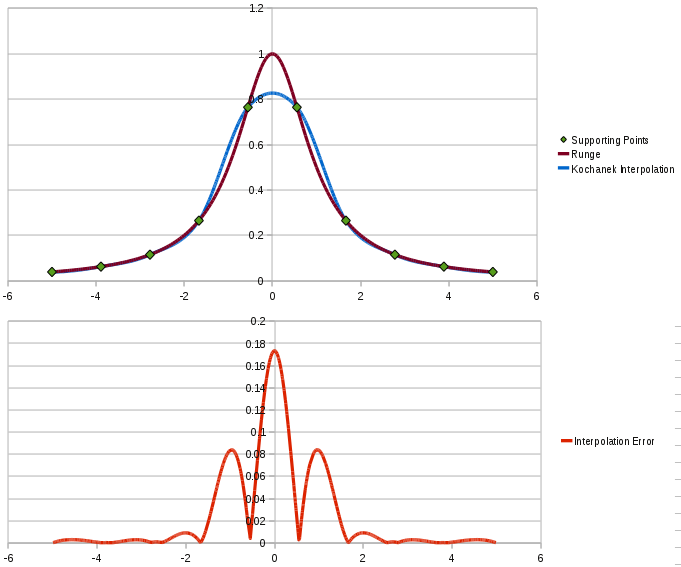
A simple example that shows how to use vtkTupleInterpolator for the purpose of interpolating 1D functions. Internally the program investigates two functions: sine and Runge function with sparsely distributed supporting points. The application uses different interpolation modes: linear, cardinal spline and Kochanek spline. Moreover, the example offers the "--csv-output" (or "-co") option which causes the program to generate CSV-sheets reflecting the interpolated data. In order to demonstrate the spline interpolation behavior at the edge regions, we use the open and closed interval spline options as well. For example, a Kochanek-interpolation of the Runge function:
Program Usage¶
./1DTupleInterpolation [](options)
-h or --help ... print this short help
-nv or --no-verbose ... no verbose messages to std::cout
-co or --csv-output ... CSV (comma separated values) file outputs
Note
optional arguments are case-sensitive!
Question
If you have a question about this example, please use the VTK Discourse Forum
Code¶
1DTupleInterpolation.cxx
//
#include <cmath>
#include <cstdlib>
#include <fstream>
#include <iostream>
#include <string>
#ifndef M_PI
#define M_PI 3.14159265358979323846
#endif
#include <vtkCardinalSpline.h>
#include <vtkKochanekSpline.h>
#include <vtkNew.h>
#include <vtkTupleInterpolator.h>
#include <ctime>
#include <vector>
#define VERBOSE(x) \
{ \
if (Verbose) \
{ \
std::cout x; \
std::cout.flush(); \
} \
}
// verbose flag
bool Verbose = true;
// CSV output flag
bool CSVOutput = false;
namespace {
/**
* Print example usage information.
**/
void PrintUsage(char* binname);
/** Runge function. **/
double FRunge(double x)
{
return 1.0 / (1.0 + x * x);
}
/** Sine function. **/
double FSin(double x)
{
return sin(x);
}
/** Execute a specific tuple interpolation method with pre-initialized tuple
* interpolator. **/
bool TestInterpolation(vtkTupleInterpolator* tupInt, double tolerance,
const char* csvFileName, double (*mathFunc)(double),
std::vector<double>& x, const std::vector<double>& y,
double N, double symmetricIntervalWidth);
} // namespace
/** \brief Demonstrate base functionality of VTK-based tuple interpolation (1D).
* Demonstrate base functionality of VTK-based tuple interpolation (1D).
*
* Application result is 0 if SUCCESSFUL.
*
* Arguments: <br>
* -h or --help ... print short help <br>
* -nv or --no-verbose ... message output (verbose) <br>
* -co or --csv-output ... CSV (comma separated values) file outputs <br>
*
* @author ---
* @version 1.2
*/
int main(int argc, char* argv[])
{
// arguments check
for (int i = 1; i < argc; i++)
{
if (std::string(argv[i]) == "-nv" || std::string(argv[i]) == "--no-verbose")
Verbose = false;
if (std::string(argv[i]) == "-h" || std::string(argv[i]) == "--help")
{
if (argc > 0)
PrintUsage(argv[0]);
else
PrintUsage(nullptr);
return EXIT_FAILURE;
}
if (std::string(argv[i]) == "-co" || std::string(argv[i]) == "--csv-output")
CSVOutput = true;
}
VERBOSE(<< "\nDemonstrating VTK-based 1-tuple interpolation capabilities.\n")
bool ok = true;
VERBOSE(<< " * Generate supporting points ... ")
bool lok = true; // local OK
// - SINE -
constexpr int N1 = 13;
std::vector<double> xs(N1, 0);
std::vector<double> ys(N1, 0);
std::ofstream csv;
if (CSVOutput)
{
csv.open("sine.csv", std::ios::out);
if (csv.is_open())
csv << "x;y\n";
else
lok = false;
}
// prepare the supporting points (sine):
for (int i = 0; i < N1; i++)
{
xs[i] = -M_PI + (double)i / (double)(N1 - 1) * (2. * M_PI);
ys[i] = FSin(xs[i]);
if (CSVOutput && csv.is_open())
csv << xs[i] << ";" << ys[i] << "\n";
}
if (CSVOutput && csv.is_open())
csv.close();
// - RUNGE -
const int N2 = 10;
std::vector<double> xr(N2, 0);
std::vector<double> yr(N2, 0);
if (CSVOutput)
{
csv.open("runge.csv", std::ios::out);
if (csv.is_open())
csv << "x;y\n";
else
lok = false;
}
// prepare the supporting points (sine):
for (int i = 0; i < N2; i++)
{
xr[i] = -5.0 + (double)i / (double)(N2 - 1) * (2. * 5.0);
yr[i] = FRunge(xr[i]);
if (CSVOutput && csv.is_open())
csv << xr[i] << ";" << yr[i] << "\n";
}
if (CSVOutput && csv.is_open())
csv.close();
ok = ok && lok;
VERBOSE(<< (lok ? "OK" : "FAILURE") << "\n")
VERBOSE(<< " * Interpolation of sine using linear method ... ")
// initialize the tuple interpolator (1D):
vtkNew<vtkTupleInterpolator> tupInt;
tupInt->SetInterpolationTypeToLinear(); // linear
tupInt->SetNumberOfComponents(
1); // 1D (NOTE: set #components AFTER interpolation-type!)
lok = TestInterpolation(tupInt, 0.04, "sin_linear_int.csv", FSin, xs, ys, N1,
M_PI);
ok = ok && lok;
VERBOSE(<< (lok ? "OK" : "FAILURE") << "\n")
VERBOSE(<< " * Interpolation of sine using cardinal spline method (open "
"interval) ... ")
// initialize the tuple interpolator (1D):
tupInt->SetInterpolationTypeToSpline(); // spline (implicit reset!)
vtkNew<vtkCardinalSpline> cardSpline;
cardSpline->SetClosed(false);
tupInt->SetInterpolatingSpline(cardSpline);
tupInt->SetNumberOfComponents(
1); // 1D (NOTE: set #components AFTER interpolation-type!)
lok = TestInterpolation(tupInt, 0.1, "sin_card_spline_open_int.csv", FSin, xs,
ys, N1, M_PI);
ok = ok && lok;
VERBOSE(<< (lok ? "OK" : "FAILURE") << "\n")
VERBOSE(<< " * Interpolation of sine using cardinal spline method (closed "
"interval) ... ")
// initialize the tuple interpolator (1D):
tupInt->Initialize(); // reset
tupInt->SetInterpolationTypeToSpline(); // spline
cardSpline->SetClosed(true);
tupInt->SetInterpolatingSpline(cardSpline);
tupInt->SetNumberOfComponents(
1); // 1D (NOTE: set #components AFTER interpolation-type!)
lok = TestInterpolation(tupInt, 0.05, "sin_card_spline_closed_int.csv", FSin,
xs, ys, N1, M_PI);
ok = ok && lok;
VERBOSE(<< (lok ? "OK" : "FAILURE") << "\n")
VERBOSE(<< " * Interpolation of sine using Kochanek spline (default setup) "
"method (open interval) ... ")
// initialize the tuple interpolator (1D):
tupInt->Initialize(); // reset
tupInt->SetInterpolationTypeToSpline(); // spline
vtkNew<vtkKochanekSpline> kochSpline;
kochSpline->SetClosed(false);
tupInt->SetInterpolatingSpline(kochSpline);
tupInt->SetNumberOfComponents(
1); // 1D (NOTE: set #components AFTER interpolation-type!)
lok = TestInterpolation(tupInt, 0.1, "sin_koch_spline_open_int.csv", FSin, xs,
ys, N1, M_PI);
ok = ok && lok;
VERBOSE(<< (lok ? "OK" : "FAILURE") << "\n")
VERBOSE(<< " * Interpolation of sine using Kochanek spline (default setup) "
"method (closed interval) ... ")
// initialize the tuple interpolator (1D):
tupInt->Initialize(); // reset
tupInt->SetInterpolationTypeToSpline(); // spline
kochSpline->SetClosed(true);
tupInt->SetInterpolatingSpline(kochSpline);
tupInt->SetNumberOfComponents(
1); // 1D (NOTE: set #components AFTER interpolation-type!)
lok = TestInterpolation(tupInt, 0.06, "sin_koch_spline_closed_int.csv", FSin,
xs, ys, N1, M_PI);
ok = ok && lok;
VERBOSE(<< (lok ? "OK" : "FAILURE") << "\n")
VERBOSE(<< " * Interpolation of Runge using linear method ... ")
// initialize the tuple interpolator (1D):
tupInt->Initialize();
tupInt->SetInterpolationTypeToLinear(); // linear
tupInt->SetNumberOfComponents(
1); // 1D (NOTE: set #components AFTER interpolation-type!)
lok = TestInterpolation(tupInt, 0.25 /* around 0! */, "runge_linear_int.csv",
FRunge, xr, yr, N2, 5.0);
ok = ok && lok;
VERBOSE(<< (lok ? "OK" : "FAILURE") << "\n")
VERBOSE(<< " * Interpolation of Runge using cardinal spline method ... ")
// initialize the tuple interpolator (1D):
tupInt->SetInterpolationTypeToSpline(); // spline (implicit reset!)
cardSpline->SetClosed(false);
tupInt->SetInterpolatingSpline(cardSpline);
tupInt->SetNumberOfComponents(
1); // 1D (NOTE: set #components AFTER interpolation-type!)
lok = TestInterpolation(tupInt, 0.15 /* around 0! */,
"runge_card_spline_int.csv", FRunge, xr, yr, N2, 5.0);
ok = ok && lok;
VERBOSE(<< (lok ? "OK" : "FAILURE") << "\n")
VERBOSE(<< " * Interpolation of Runge using Kochanek spline method ... ")
// initialize the tuple interpolator (1D):
tupInt->Initialize(); // reset
tupInt->SetInterpolationTypeToSpline(); // spline (implicit reset!)
kochSpline->SetClosed(false);
tupInt->SetInterpolatingSpline(kochSpline);
tupInt->SetNumberOfComponents(
1); // 1D (NOTE: set #components AFTER interpolation-type!)
lok = TestInterpolation(tupInt, 0.18 /* around 0! */,
"runge_koch_spline_int.csv", FRunge, xr, yr, N2, 5.0);
ok = ok && lok;
VERBOSE(<< (lok ? "OK" : "FAILURE") << "\n")
VERBOSE(<< "Application result: ")
if (ok)
{
VERBOSE(<< "OK\n\n")
return EXIT_SUCCESS;
}
else
{
VERBOSE(<< "FAILURE\n\n")
return EXIT_FAILURE;
}
}
namespace {
/**
* Print example usage information.
**/
void PrintUsage(char* binname)
{
std::string progname = "<binary-name>";
if (binname)
progname = std::string(binname);
std::cout << "\n";
std::cout << " *** E X A M P L E U S A G E ***\n";
std::cout << "\n";
std::cout << progname << " [options]\n";
std::cout << "\n";
std::cout << " -h or --help ... print this short help\n";
std::cout << " -nv or --no-verbose ... no verbose messages to std::cout\n";
std::cout << " -co or --csv-output ... CSV (comma separated values) file "
"outputs\n";
std::cout << "\n";
std::cout << " NOTE: optional arguments are case-sensitive!\n";
std::cout << "\n";
std::cout << " Author: ---\n";
std::cout << " Affiliation: ---\n";
std::cout << "\n";
}
/** Execute a specific tuple interpolation method with pre-initialized tuple
* interpolator. **/
bool TestInterpolation(vtkTupleInterpolator* tupInt, double tolerance,
const char* csvFileName, double (*mathFunc)(double),
std::vector<double>& x, const std::vector<double>& y,
double N, double symmetricIntervalWidth)
{
bool ok = true;
std::ofstream csvint;
if (CSVOutput)
{
csvint.open(csvFileName, std::ios::out);
if (csvint.is_open())
csvint << "x;y;e\n";
else
ok = false;
}
double yt[1];
for (int i = 0; i < N; i++) // re-define supporting points
{
yt[0] = y[i];
tupInt->AddTuple(x[i], yt);
}
// draw random samples from interval and test against mathFunc:
for (int i = 0; i < 1000; i++)
{
double f = (double)(rand() % 100001) / 100000.;
double xi = (f * 2.0 - 1.0) * symmetricIntervalWidth;
double yi[1];
tupInt->InterpolateTuple(xi, yi);
double ei = std::abs(yi[0] - mathFunc(xi));
// we have a tolerance within [-PI;+PI] - empirical!
if (xi >= -symmetricIntervalWidth && xi <= symmetricIntervalWidth &&
ei > tolerance)
ok = false;
if (CSVOutput && csvint.is_open())
csvint << xi << ";" << yi[0] << ";" << ei << "\n";
}
if (CSVOutput && csvint.is_open())
csvint.close();
return ok;
}
} // namespace
CMakeLists.txt¶
cmake_minimum_required(VERSION 3.12 FATAL_ERROR)
project(1DTupleInterpolation)
find_package(VTK COMPONENTS
CommonComputationalGeometry
CommonCore
InteractionStyle
RenderingContextOpenGL2
RenderingCore
RenderingFreeType
RenderingGL2PSOpenGL2
RenderingOpenGL2
)
if (NOT VTK_FOUND)
message(FATAL_ERROR "1DTupleInterpolation: Unable to find the VTK build folder.")
endif()
# Prevent a "command line is too long" failure in Windows.
set(CMAKE_NINJA_FORCE_RESPONSE_FILE "ON" CACHE BOOL "Force Ninja to use response files.")
add_executable(1DTupleInterpolation MACOSX_BUNDLE 1DTupleInterpolation.cxx )
target_link_libraries(1DTupleInterpolation PRIVATE ${VTK_LIBRARIES}
)
# vtk_module_autoinit is needed
vtk_module_autoinit(
TARGETS 1DTupleInterpolation
MODULES ${VTK_LIBRARIES}
)
Download and Build 1DTupleInterpolation¶
Click here to download 1DTupleInterpolation and its CMakeLists.txt file. Once the tarball 1DTupleInterpolation.tar has been downloaded and extracted,
cd 1DTupleInterpolation/build
If VTK is installed:
cmake ..
If VTK is not installed but compiled on your system, you will need to specify the path to your VTK build:
cmake -DVTK_DIR:PATH=/home/me/vtk_build ..
Build the project:
make
and run it:
./1DTupleInterpolation
WINDOWS USERS
Be sure to add the VTK bin directory to your path. This will resolve the VTK dll's at run time.